数据结构笔记：二叉树

https://oi-wiki.org/ds/bst/

二叉搜索树

BST, Binary Search/Sort Tree
左子节点 < 父节点 < 右子节点，所以右子树的所有值必 > 左子树的所有值。
插入时从上往下按上述规则遍历，直至空节点创建子节点。
删除有两个子节点的节点时，替换为当前节点的中序后继或前驱，即右子树中的最左边（最小值）节点或左子树中的最右边（最大值）节点。时间复杂度是树的深度即 O(logN) ，最差情况从树退化为单链表 O(N) ，所以需要自平衡的二叉搜索树。

template<typename T>
struct TreeNode {
	TreeNode<T>* left;
	TreeNode<T>* right;
	T data;
	TreeNode(T val = T{}) :data{ val }, left{ nullptr }, right{ nullptr } {}
};

template<typename T, typename Compare = std::less<T>>
class BST {
	TreeNode<T>* root;
	void Destory(TreeNode<T>* node) {
		if (!node) return;
		Destory(node->left);
		Destory(node->right);
		delete node;
	}
	Compare isLessThan; // 使用函数对象替换 "<"，自定义比较规则
public:
	BST() :root{ nullptr } {}
	~BST() { Destory(root); }
	//增
	void Insert(const T& val) { //左值（拷贝）迭代
		if (!root) {
			root = new TreeNode<T>{ val };
			return;
		}
		else {
			TreeNode<T>* cur = root;
			TreeNode<T>* parent = nullptr;
			while (cur) {
				if (!isLessThan(val, cur->data) && !isLessThan(cur->data, val)) return;
				parent = cur;
				isLessThan(val, cur->data) ? cur = cur->left : cur = cur->right;
			}
			isLessThan(parent->data, val) ? parent->right = new TreeNode<T>{ val } : parent->left = new TreeNode<T>{ val };
		}
	}
	void Insert(T&& val, TreeNode<T>*& root) { //右值（移动）递归
		if (!root) {
			root = new TreeNode<T>{ std::move(val) };
			return;
		}
		else if (isLessThan(val, root->data)) {
			Insert(std::move(val), root->left);
		}
		else if (isLessThan(root->data, val)) {
			Insert(std::move(val), root->right);
		}
		else return; //重复元素
	}
	//删
	void remove(const T& val) { //迭代
		if (!root) return;
		TreeNode<T>* cur = root;
		TreeNode<T>* parent = nullptr;
		while (isLessThan(val, cur->data) || isLessThan(cur->data, val)) {
			parent = cur;
			isLessThan(val, cur->data) ? cur = cur->left : cur = cur->right;
			if (!cur) return;
		}
		if (cur->left && cur->right) { //双子节点
			TreeNode<T>* key = cur;
			parent = cur;
			cur = cur->right;
			while (cur->left) {
				parent = cur;
				cur = cur->left;
			}
			key->data = cur->data;
			if (parent->left == cur) {
				parent->left = cur->right;
			}
			else {
				parent->right = cur->right;
			}
			delete cur;
		}
		else if (!cur->left && !cur->right) { //无子节点
			if (!parent) root = nullptr;
			else {
				parent->left == cur ? parent->left = nullptr : parent->right = nullptr;
				delete cur;
			}
		}
		else { //单子节点
			auto* t = cur;
			cur->left ? cur = cur->left : cur = cur->right;
			if (!parent) root = cur;
			else (parent->left == t ? parent->left : parent->right) = cur;
			delete t;
		}
	}
};

AVL树

平衡因子为 左子树高度 - 右子树高度，值严格为±1,0，即左右严格平衡。
增删改查时间复杂度都为 O(logN) 。
查询高效，但频繁地插入和删除时旋转操作频繁，开销大。
常用于：内存管理、文件系统管理、优先队列、路由算法。

插入旋转

LL右旋，RR左旋（根节点）；LR左旋+右旋，RL右旋+左旋（子节点+根节点）。

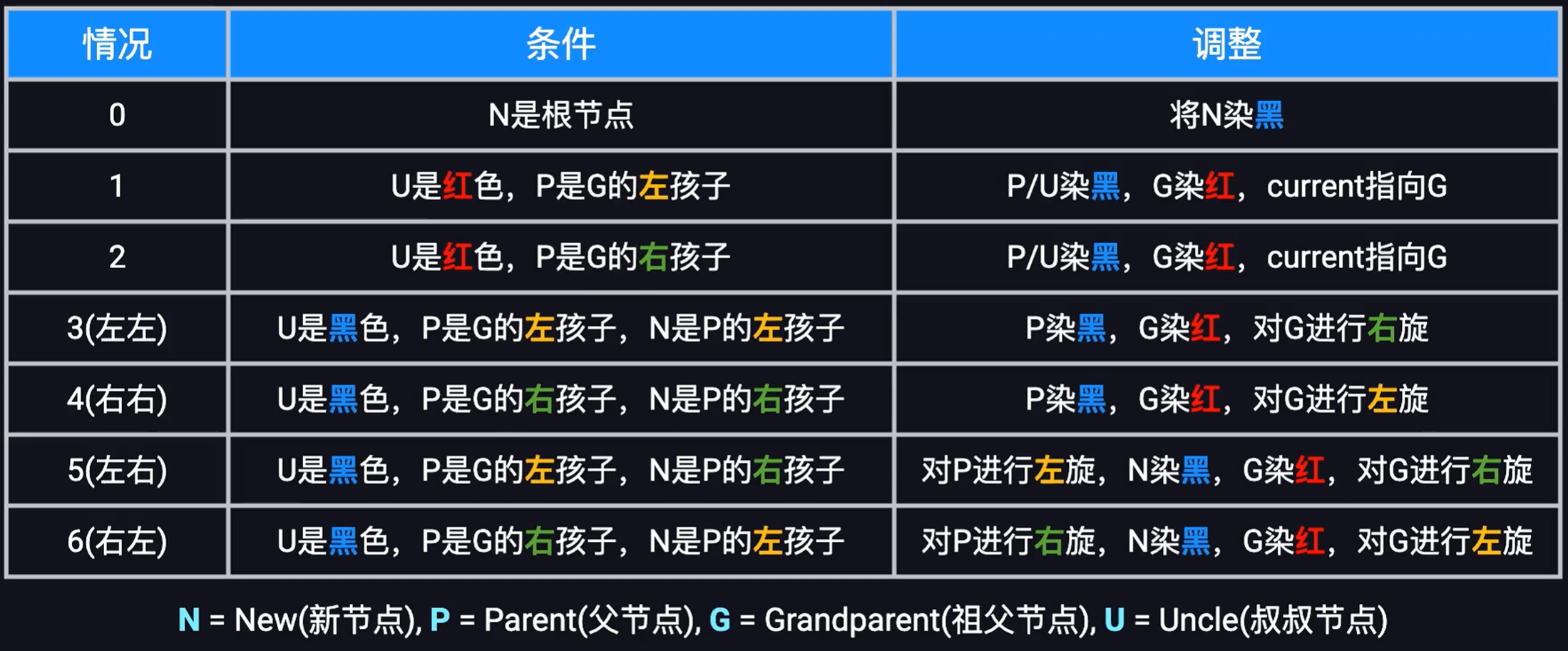
红黑树

弱平衡，O(logN) 。
插入删除高效。
常用于语言标准库实现，操作系统 Linux 管理虚拟内存 VMA， 网络系统 Linux 的 ipset 快速存储和匹配 IP 规则。
节点定义时增加颜色和父节点成员变量。

规则：

① 每个节点或红或黑。
② 根节点是黑色。
③ 所有叶（NIL）哨兵节点为黑色。
④ 如果节点是红色，其子节点都是黑色。
⑤ 从任意节点到其每个叶子的路径，都包含相同数量的黑色节点。
根节点到叶子节点的最长路径，不会超过最短路径的2倍。
左旋使根节点下降，右子节点上升，原右子节点的左子树变为原根节点的右子树。右旋同理。

插入

时间复杂度为 O(logN)，插入＋修复。
① 按照二叉搜索树的规则插入新的红色节点
② 若违反规则，则通过重新着色+旋转来修复
修复：逐层向上修复，根节点直接改为黑色。