堆的定义

是完全二叉树：只允许最后一行不为满，且最后一行必须从左往右排序，最后一行元素之间不可以有间隔。特性适合数组存储。

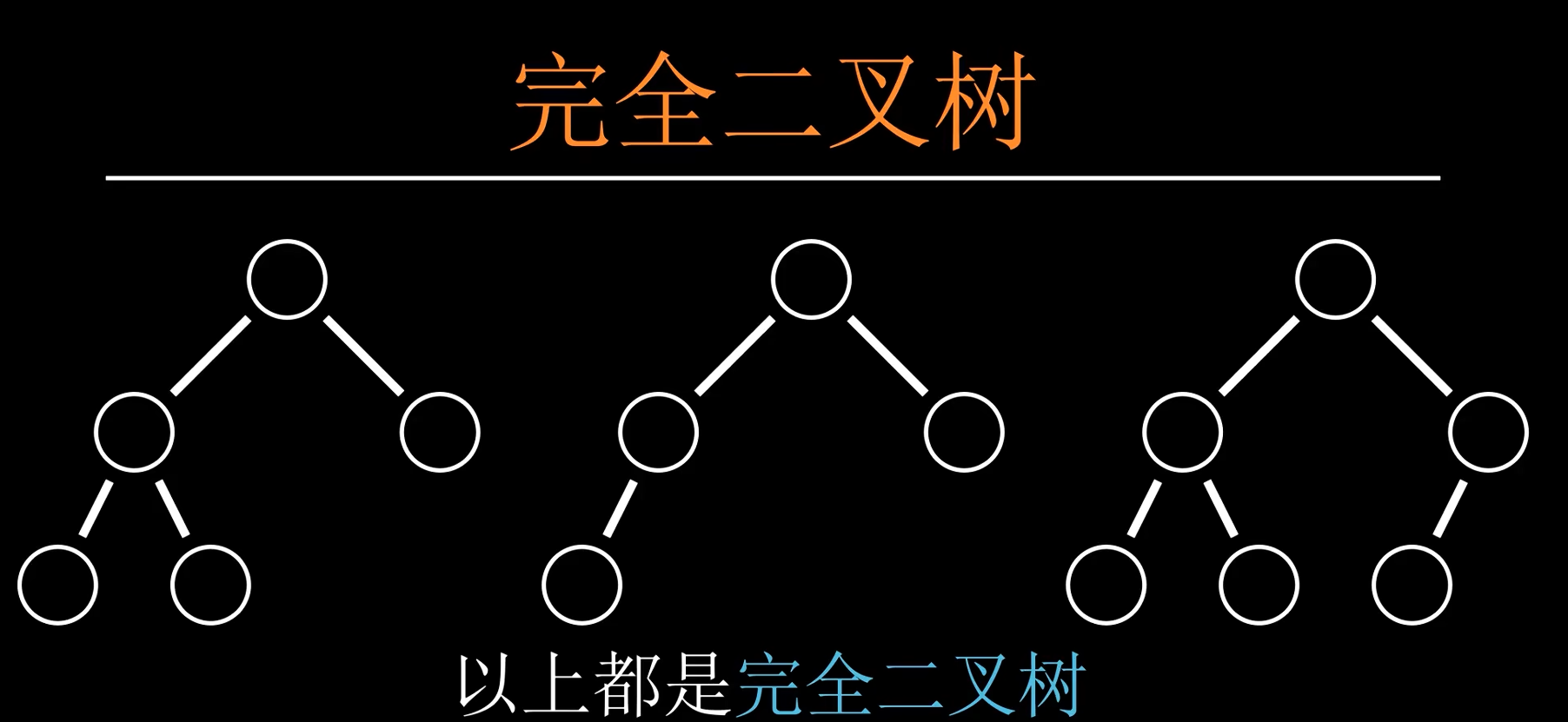
层序遍历给节点编号，元素存入数组对应下标，下标节点为 i ，其子节点则为 2i+1 2i+2 。

堆的基本操作

上滤（上浮） / 下滤（下沉）

下滤

根节点向下调整

  • 若（根）节点元素小于其最大子节点，则交换，直至该元素所在节点大于其所有子节点或移动到底部（无子节点），形成大根堆。
  • 复杂度为 O(logN) 。
    自下而上建堆，从倒数第二行父节点开始向下调整，复杂度为 O(N) 。

上滤

子节点向上调整

  • 与父节点比较，大于父节点则交换，直到无法上移。
  • 主要用于插入新元素到堆尾，复杂度为 O(logN) 。
    自顶向下建堆，每次插入到堆尾后向上调整，复杂度为 O(NlogN) 。

堆的应用

优先队列 priority_queue

默认为最大堆
弹出堆顶元素后，堆尾元素移至根节点，重新进行上滤或下滤操作直至有序。

  • 堆排序就是把优先队列元素依次弹出，为降低空间复杂度，实际排序时堆顶弹出的元素与堆尾元素交换并存放，最终形成的树做层序遍历便是有序的。时间复杂度为 O(NlogN) 。

根据后者 b 的大小判断

想要的堆类型 比较函数 Compare(a,b) 含义
大顶堆（默认） a < b a 小 → a 优先级低，堆顶是最大
小顶堆 a > b a 大 → a 优先级低，堆顶是最小